非監督式的學習，資料上沒有標籤，也就是沒有答案，很適合還不知道要找出什麼問題，透過聚類來看出資料的相關性，比如說 Netflix 的客戶觀看影片傾向。或是找出異常性的資料。

聚類（Clustering）

根據資料的類似度，將資料分類的手法。就是我們說的物以類聚，人以群分。

K平均（K-means）

把 n 個點分成 k 個類別，使得每個點都屬於離它最近的重心（centroid）所屬類別，作為聚類的標準。屬於無階層的聚類。

步驟如下：

1. n 個點
   
2. 將 k 個重心放到任意位置，這邊想分3類， k=3
   
3. 每個資料找最近的重心，分成3類
   
4. 根據各個聚類的平均，去更新重心的位置
   
5. 重複步驟3和4
   • 重複3. 找最近的重心分類
     
   • 重複4. 更新重心位置
     
     中心位置不會再變化，聚類完成

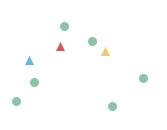
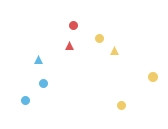
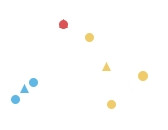
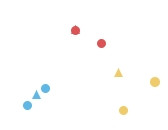
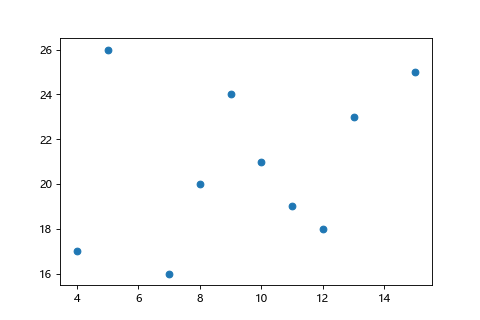
實際上用程式跑看看：

• 隨機產生 10 筆資料
  
• 分 3 類
  

沃德法（Ward's method）

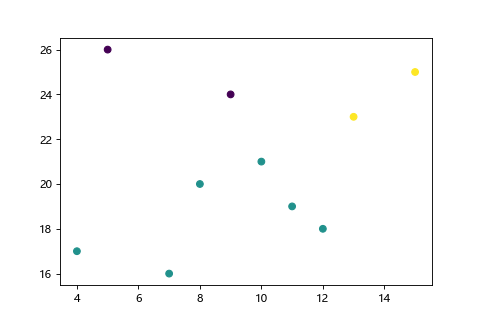
階層式聚類。

1. n 個點
   
2. 兩兩合體
   
3. 直到成為目標的聚類數（比如1）
   • 重複2.
     
   • 變成一個大類，結束
     

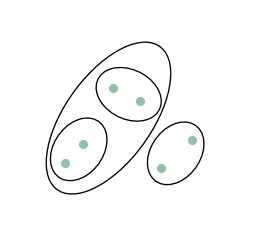
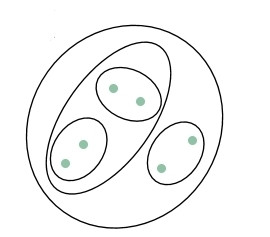
這樣的階層構造可以用樹狀圖（dendrogram）表示，所以叫階層式聚類。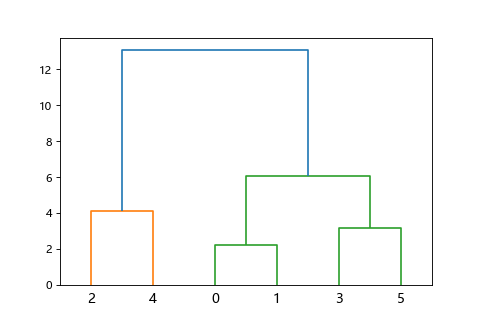

試著用程式產生隨機6筆資料的樹狀圖。

主題模型（Topic Model）

一份資料有多個聚類，只是類別的比重或大或小。比方說一篇日本旅遊部落客的遊記，可能同時有多個類別「日本」，「旅遊」，「美食」，「飯店」等，其中美食的比例可能佔最大。代表性的手法有隱含狄利克雷分佈（LDA，Latent Dirichlet Allocation），常用来做自然語言處理（NLP，Natural Language Processing）的文章分類。

• 一份資料可能會有好幾個主題（Topic），每個主題都有數個重要的關鍵字（Word）。
• 關鍵字可以同時出現在好幾個主題上面。

透過關鍵字出現的頻率，決定這份資料每個主題的占比大小。

舉例來說，有一份客戶的線上觀看影片紀錄（當作資料），如果他常看的節目名稱（關鍵字），有陰屍路，活屍末日，美國恐怖故事，偶爾觀看六人行，宅男行不行，代表這個客戶的喜愛主題（Topic），恐怖類占最大宗（陰屍路，活屍末日，美國恐怖故事），活屍類次之（陰屍路，活屍末日），還有一點喜劇類（六人行，宅男行不行）。

推薦系統（Recommendation System）

前面談到的主題模型，電商平台如果把客戶的消費行為紀錄當成資料，產品當成關鍵字的話，就可以很清楚要推薦什麼產品給客人了。可以推薦和他相類似的人（具有大部分相同主題）買過什麼產品。

這種手法叫做協同過濾（Collaborative filtering），你雖然沒買過，但是和你相像的使用者曾經買過的東西你可能也會有興趣。這種手法需要事前累積一定程度的其他使用者的資料，否則無法做推薦，這個問題叫做冷啟動問題（Cold start problem）。

而為了迴避冷啟動問題，還有一種推薦方式是藉由物品的特徵，推薦和你買過的東西相類似的商品，這種手法叫做內容導向推薦（Content based filtering），常常會和協同過濾一併使用。

網路購物時常出現的，「和你同樣買了這個商品的客人也買了這些東西」，「你放到購物車的產品還有其他類似的商品」就是這些手法的運用。

關聯規則（Association rule）

提到了推薦系統就要來講一下關聯規則，也就是我們常說的購物籃分析（Basket Analysis）。透過客戶的購物籃使用下面三個統計量找出商品之間的關聯。通常採用的是 Apriori 算法。

• 支持度（Support）
  A 和 B 同時被購買的機率。
  比如某速食店單日有1000筆銷售，同時買可樂和薯條有200筆，買可樂和漢堡有100筆。則可樂和薯條支持度有20％，可樂和漢堡支持度有10％。可以先用來確認兩個產品的同時出現頻率是否足夠。
  

• 信賴度（Confidence）
  購買 A 後購買 B 的機率。
  比如某速食店單日有可樂400筆銷售，同時買可樂和薯條有200筆，買可樂和漢堡有100筆。則可樂和薯條的信賴度有50％，可樂和漢堡的信賴度有25％。代表買可樂也買薯條的關聯性比漢堡強，可以對可樂和薯條做組合包銷售。作為主要的關聯規則。
  

• 提升度（Lift）
  確認 A 和 B 的相關性。
  A 和 B 同時購買的機率是否大於 A 和 B 單獨被購買的機率。
  大於1為正相關有提升效果，等於1為無影響，小於1為負相關反而變糟。
  用來作為評價指標，避免信賴度很高的假象。比如說可樂和薯條的信賴度很高，但有可能買了可樂也買薯條的人雖然多，但其實就算不買可樂的人也一樣會買薯條。
  

由此衍生出：

• 相關性高的商品綁在一起促銷，提高購買意願。
• 相關性高的商品可以擺在一起方便客戶拿取。
• 相關性高的商品可以在購物網站上做推薦。

主成分分析（PCA，Principal Component Analysis）

核心摡念就是化繁為簡，當數個特徵有強相關時可以組合在一起在較少的維度上描述資料。

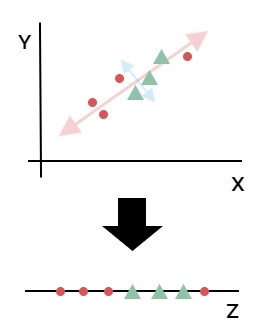
如下圖資料大部分都分散在紅色對角線上，而藍色對角線的分散則沒有很明顯。也就是這些資料都可以透過紅色直線來解釋，把2維資料壓縮成1維資料。這種2維平面降成1維直線，3維空間降成2維平面的手法我們稱作降維。而壓縮過後的特徵稱作主成分。

舉例來說就像是身高，體重，體脂率，骨骼比例這4個特徵壓縮成像男生，像女生兩種特徵。

這邊的維度=特徵數量，2維平面就是有2個特徵（2個軸），3維空間就是有3個特徵（3個軸）。降維也就等於特徵數量減少。

降維（dimension reduction）

降維因為減少了特徵的數目，有2個用處

• 解決維度的詛咒（Curse of dimensionality）
  維度的詛咒是指隨著特徵的數目增加，所需的訓練資料量呈指數成長，導致學習非常耗時。當有很多特徵時，降維可以使學習更有效率。

• 讓高維度變成低維度達到可視化，幫助理解和解釋。
  因為物理空間只到3維，再上去的高維度就難以想像了。

降維的其他常見手法還有多維標度（MDS，Multi-Dimensional Scaling）和奇異值分解（SVD，Singular Value Decomposition）。可視化則常用可以做非線性降維的 t-隨機鄰近嵌入法（t-SNE）。

補充資料

• 範例程式 - K-means
• 範例程式 - Ward's Method
• 範例程式 - Apriori
• 範例程式 - PCA 降維後可視化
• Airbnb 透過 LDA 做個人化推薦

立即複習

1. K 平均屬於有階層還是無階層的聚類？
2. Ward's Method 可以形成什麼圖，所以被稱為有階層的聚類？
3. LDA 是針對 自然語言處理 做文章分類，屬於什麼模型常用的手法？
4. 協同過濾是推薦別人買過的東西，但是需要事先累積資料的問題叫做？
5. PCA 主要是透過降維來減少什麼的數量？

參考資料

• Wikipedia - Association_rule
• 機械学習と主成分分析
• キカペン - 教師なし学習